Figure 1: Adiabatic hyperspherical pontential curves for 4He3.
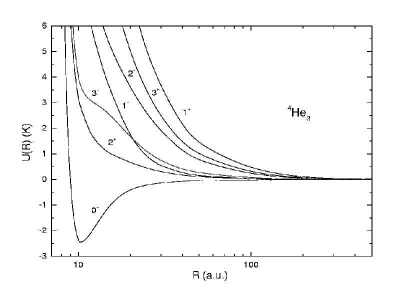
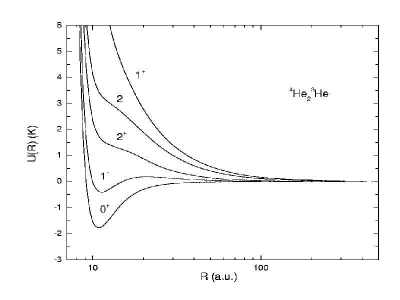
Figure 2: Adiabatic hyperspherical pontential curves for 4He23He.
Hyperspherical Calculations of He Trimer with Non-zero Angular Momenta
Teck G. Lee, B.D. Esry and C.D. Lin
Department of Physics, Kansas State University, Manhattan, Kansas 66506, U.S.A.
The properties of very weakly bound small He clusters have been examined in a variety of theoretical and experimental studies. For helium trimers, practically all theoretical calculations that have been carried out dealt with states of zero total angular momentum. It is known that there are two J=0 bound states for 4He3, and thus it has been speculated whether there are possible J > 0 excited states.
Based on a simple rigid rotor model, an estimate of the rotational energy using parameters from the 4He3 ground state suggests that a state with J=1 is close to being bound. However, such a simple estimate can be grossly in error since quantum statistics are not taken into account. In the present work, the adiabatic hyperspherical method has been employed to investigate the possible existence of bound states of triatomic helium molecules for J>0. By including only the pair interactions between He atoms, we solved the Schrodinger equation in hyperspherical coordinates within the adiabatic approximation. The adiabatic channel functions are calculated using B-spline functions in the body-frame of the molecule. From the adiabatic hyperspherical potential curves we search for the existence of bound states for J>0.
Figure 1 shows the adiabatic potential curves with respect to the hyperradius. From these potential curves, except for J=0, the curves are repulsive and therefore we conclude that no J > 0 bound states are possible for the 4He3 system. In figure 2, we show potential curves for the 4He23He system, and we found no bound states as well. It is interesting to note the difference in the order of Jπ curves in the two systems. This difference is a result of quantum statistics. In figure 2, 4He23He has two bosons and one fermion, hence the wave function needs to be symmetric under the exchange of the two bosons only. For 4He3 the wave function must be symmetric under the interchange of any pair of He atoms. This study clearly demonstrates that quantum symmetry governs the order of these Jπ curves for the diffuse molecular systems.
Figures:


References:
1. B. D. Esry, C. D. Lin and C. H. Greene, Phys. Rev. A. 54, 394 (1996).
2. W. Schöllkopf and J. P. Toennies, Science 226,1345 (1994).
3. L.W. Bruch, J. Chem. Phys. 110, 2410 (1999)
This work was supported by the
Chemical Sciences, Geosciences and Biosciences Division,
Office of Basic Energy Sciences,
Office of Science,
U.S. Department of Energy.
Submitted to ICPEAC 2001, July 2001 in Santa Fe, NM.
This abstract is also available in Postscript or Adobe Acrobat formats.
|
|