Monte Carlo hyperspherical description of cluster excited states
D. Blume 1 , C. H. Greene 2 , B. D. Esry 3 , and G. J. Hanna 1
1) Department of Physics, Washington State University, Pullman, WA 99164-2814
2) Department of Physics and JILA, University of Colorado, Boulder, Colorado 80309-0440
3) Department of Physics, Kansas State University, Manhattan, Kansas 66506
Though a variety of approaches can be used to calculate ground state properties,
widely applicable methods for the calculation of excited state energies and wave functions
of many-body systems are still lacking. For example, Monte Carlo (MC) methods such as
the variational Monte Carlo (VMC) method, the diffusion quantum Monte Carlo (DMC)
method, and the Green's function Monte Carlo (GFMC) method show a favorable scaling
of the computational effort with the number of particles when used to calculate ground
state properties, but they cannot readily be extended to calculate excited state properties.
This talk outlines a new approach to treating excited states of many-body systems by
combining MC methods with the adiabatic hyperspherical description. Application of this
new approach to helium clusters, and also heavier rare gas clusters, will be presented.
Bosonic helium systems - i.e. liquid bulk 4He, two-dimensional
4He films, and finite
size 4HeN clusters - have been studied extensively.
4HeN clusters, which are investigated
here, offer a wealth of interesting physics by virtue of its weak van der Waals attraction,
and its light atomic mass. Numerous theoretical calculations have determined the existence,
size, and energetics of small
4HeN clusters in their ground state. However, only
comparatively few predictions - mostly for the 4He trimer and tetramer, and for larger
clusters with N = 20 or more atoms - for excited state behavior exist. Here, we report on
excited state calculations for 4HeN clusters with up to N = 10 atoms,
which thus narrow
the gap between small cluster and "large cluster" treatments. Our MC calculations predict
the number of J = 0 (rotationless angular momentum) bound states for
4HeN clusters, and
also the 4He + 4HeN-1 elastic scattering lengths.
The J=0 many-body Schrödinger equation for the nuclear coordinates is solved
numerically by combining Monte Carlo methods with the adiabatic hyperspherical
approximation. Adopting the adiabatic approximation is motivated
by the following two main arguments. First, the separation into one radial coordinate,
the hyperradius R, and (3N-1) angular coordinates, collectively denoted by Ω,
results in an effective one-dimensional potential curve U(R), which in turn allows
the approximate calculation of excited states. Second, the effective one-dimensional
curve allows us to use our intuition to
interpret the size of the system, as well as showing the regions where transitions
occur between one
geometrical configuration and another. As an example, Fig. 1 shows the lowest adiabatic
potential curves U(R) for 4HeN clusters with N = 3-10, together
with the lowest radial wave functions, and the ground state energies. Excited state
energies can be readily calculated by solving the one-dimensional Schrödinger equation
in the R coordinate with effective mass that feels the interaction potential U(R).
The characteristics of weakly bound helium clusters are compared with those for
spin-polarized tritium clusters, in the following denoted by (T↑)N.
It turns out that spin-polarized tritium clusters are even more weakly bound
than helium clusters. Of particular interest is furthermore the lowest quartet state
of the tritium trimer, which we predict to
be a Borromean or halo state. We also predict a Feshbach resonance for two high-field
seeking |F,mF> = |0, 0> tritium atoms (F denotes the total angular momentum,
and mF
the magnetic quantum number of this state), which could lead to unexpected physics when
manipulating (T↑)N cluster formation through an external magnetic field.
To illustrate the highly quantum (sometimes referred to as "liquid-like") behavior of
4HeN clusters further, we contrast the behavior of
4HeN clusters to that of heavier rare
gas clusters, i.e., bosonic neon and argon clusters. These heavier rare gas clusters exhibit
a manifold of geometrically and energetically distinct isomers, each of which shows
non-negligible zero point energy. These isomers can be identified in the adiabatic hyperspherical
potential curves. Comparison with adiabatic potential curves for 4HeN
clusters underlines
the unique behavior of helium clusters.
Figures:
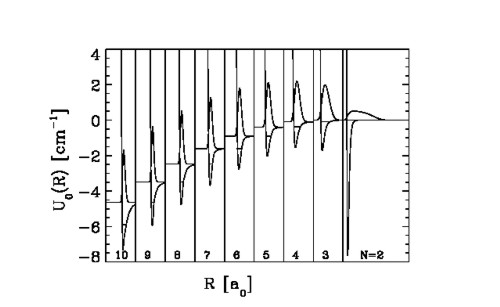
Figure 1:
Effective potential curves U0(R), wave functions F
BO00(R), and ground state
energies E0
for HeN clusters with N = 3 through 10 together with the two-body He-He potential, the exact dimer
ground state wave function, and the He dimer ground state energy. The hyperspherical radius R (R is
identical to the interparticle distance r12 for the He dimer) has a logarithmic scale; for the
N = 3 through 10 plots,
R∈[3 a0, 150 a0],
while for the N = 2 plot,
R∈[3 a0, 1200 a0].
Note that U0(R)
of the cluster with N atoms
approaches the ground state energy E0
of the next smaller cluster with N-1
atoms for large R
(1 a0 = 0.529 Å).
This figure is taken from Ref. [1].
References:
[1] D. Blume and C. H. Greene, J. Chem. Phys. 112, 8053 (2000)
This work was supported by the National Science Foundation.
Submitted to the Ugo Fano Memorial Symposium, July, 2002 in Cambridge, MA.
This abstract is also available in
Postscript or
Adobe Acrobat formats.
