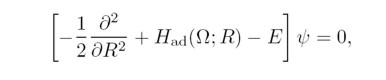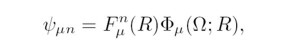Hyperspherical approach to three- and four-electron atomic systems
Toru Morishita
Department of Applied Physics and Chemistry, The University of Electro-Communications,
1-5-1 Chofu-ga-oka, Chofu-shi, Tokyo 182-8585, Japan
C. D. Lin
Department of Physics, Kansas State University, Manhattan, KS 66506, USA
Hyperspherical coordinates were first introduced by
Fano and his coworkers [1,2] to understand the basic
properties of doubly excited states of helium atoms. In
the past several decades, this approach has been improved
and extended to a broad range of few-body atomic
and molecular systems. In this work, we present our
recent progress on the understanding of electron correlations
mainly in triply excited states of atoms. We also
present a new development of the hyperspherical approach
to a four-electron atomic system.
In the hyperspherical method, 3N dimensional configuration
space of an N-electron atom with the nucleus
at the center is parametrized by a hyperradius
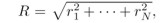characterizing the mean square of
the size of the system, and by (3N-1) bounded hyperangles
Ω, describing the relative positions of the electrons.
In hyperspherical coordinates, the Schrödinger equation
can be written as
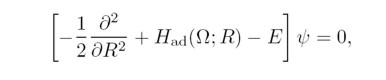
where Had(Ω;R) is the adiabatic
Hamiltonian which depends
parametrically on R. Within the adiabatic approximation
introduced by Macek [3], the total wavefunction
for the n-th state in channel μ can be written as
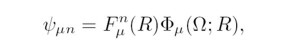
where Fμn(R) is the
hyperradial function which measures
the size of the state; Φμ(Ω;R)
is the hyperspherical adiabatic
channel function, which contains all the information
about electron correlations for states within channel µ.
The channel function
Φμ(Ω;R)
and its associated adiabatic
potential Uμ(R)
are obtained by solving the adiabatic
eigenvalue problem at each R,
We solved this eigenvalue problem for three-electron
atomic systems for each
2S+1Lπ
symmetry [4], and for a four-electron atomic system.
As an example of three-electron atoms, we show the
adiabatic potential curves for
Li(2Se) states in Fig. 1.
At large R, each curve approaches the two electron Li+
states: The potentials can be classified into three groups
by their asymptotic limits. The first group consists
of a single curve - the lowest curve, labeled ‘I’ in
Fig. 1. This curve approaches the
Li+(1s2 1Se)
state
as R → ∞. This curve supports the ground state and
the
1s2ns 2Se (n ≥ 2)
singly excited states. The second
group, labeled ‘II’ in Fig. 1, consists of potential curves
that approach the
1snl (n ≥ 2)
singly excited states of
Li+ at large R.
These curves support doubly excited states.
The third group, labeled ‘III’, consists of potential
curves that approach the
nln'l' (n, n' ≥ 2)
doubly excited
states of Li+ at large R. These curves support triply
excited states. Clearly, the avoided crossings among the
di.erent groups are very sharp. Thus, the hyperspherical
adiabatic channels can be used to separate singly, doubly,
and triply excited states.
To identify the features that characterize the adiabatic
channels among the triply excited states, we examined
the channel functions, Φ’s. We classify triply excited states
of Li in the 2l2l'2l" and the 2l2l'3l" manifolds by
visualizing the channel functions in the body-fixed frame.
We found that angular correlations play an important
role in characterizing the 2l2l'2l" intrashell states. By
examining the wavefunctions of the three electrons at
the same distance from the nucleus, we found that these
intrashell states are distinguished by their distributions
in the three relative angles (See Fig. 2 for the definition
of the angles). By examining the wave functions in the
body-fixed frame, we identi.ed three basic modes of the
three relative angles. In Fig. 3, we plotted the equidensity
surfaces of internal wavefunctions for the 2l2l'2l" intrashell
states. These surfaces can be grouped clearly
into three types. In fact, the major distinction being
that in group A, the three electrons form a coplanar e-
quilateral triangle; in group B they form an equilateral
triangle but not coplanar, and in group C the three electrons
are coplanar but not allowed to make an equilateral
triangle. The ‘forbidden region’ for the latter two groups
originates from the quantum symmetry in that a state
with well-defined quantum numbers L, S, and π would
incur nodal surfaces in a multidimensional wavefunction.
We also examined the internal wavefunctions for the
2l2l'3l" intershell triply excited states of Li. For these
states, radial correlations as well as angular correlations
play an important role in the classification. A new quantum
number was introduced to describe the symmetric
and antisymmetric stretches between the two inner electrons
with the third one.
The next major step is to understand the four-electron
atomic systems, where one can expect much richer electron
correlation effects. We implemented a pilot calculation
for Be within the s4 configurations,
and resulting
hyperspherical adiabatic potential curves for the
1Se
symmetry are shown in Fig. 4. The general appearance
of the adiabatic potentials does not di.er markedly from
those of three-electron atoms such as Li. At large R,
each curve converges to the three-electron Be+ states.
The groups labeled ‘I’, ‘II’, and ‘III’ consist of potential
curves that support singly, doubly, and triply excited
states of Be, respectively, and they are similar to the
three-electron systems as shown in Fig. 1. In addition
to these three groups, we can clearly observe the fourth
group, labeled ‘IV’. The curves in the fourth group converge
to the triply excited states of Be+ and they support
quadruply excited states of Be. We note that the avoided
crossings among the different groups are very sharp. This
suggests that quadruply excited states of Be are rather
stable against autoionization to singly, doubly, and triply
ionized states of Be. Our next goal is to examine the hyperspherical
potentials including the effects from higher
angular momentum states and to classify the quadruply
excited states.
Figures:
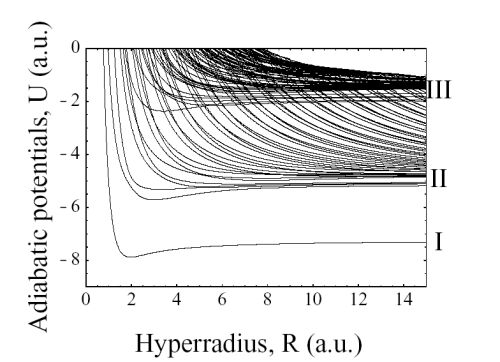
Figure 1:
Hyperspherical adiabatic potentials for the
2Se
symmetry of Li.
Figure 2:
Definition of the three angles used to describe the three
electrons on a sphere.The three electrons form a σ plane. On the
plane (the right figure) the three electrons are confined to a circle.
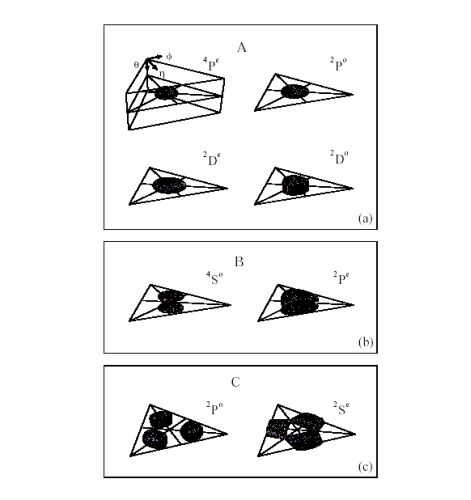
Figure 3:
The equidensity surface plots of the three-electron wavefunctions for the
eight intrashell states at
r1 = r2 = r3.
The surface represents 60% of the maximum density.
Each ‘slice’ represents the whole range of the three angles
(0≤θ≤π, 0≤η≤π, -η≤φ≤η).
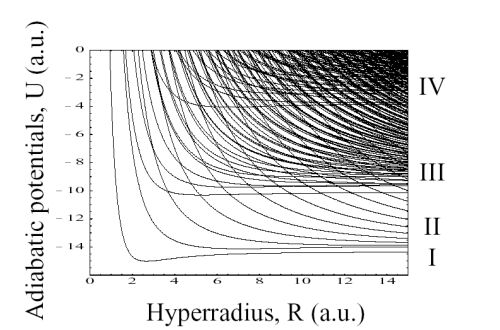
Figure 4:
Hyperspherical adiabatic potential curves for the
1Se symmetry of Be within the
s4 configuration.
References:
[1] W. Cooper, U. Fano, and F. Prats, Phys. Rev. Lett. 10, 518 (1963).
[2] U. Fano, Phys. Today 29, 32 (1976).
[3] J. Macek, J. Phys. B1, 831 (1968).
[4] T. Morishita and C. D. Lin,Phys. Rev. A, 57, 1835 (1999).
This work was supported by the
Chemical Sciences, Geosciences and Biosciences Division,
Office of Basic Energy Sciences,
Office of Science,
U.S. Department of Energy.
Submitted to the Fano Memorial Symposium, July 2002 in Cambridge, MA.
This abstract is also available in
Postscript or
Adobe Acrobat formats.
